< home

about the program

how to apply

projects

meet our faculty

life@fairfield

contact us

Projects 2016

Students will work on one of the following research topics:

Factorization Properties of Rings and Monoids
Faculty Mentor: Paul Baginski

Many areas of mathematics involve the process of factoring one object into a product of simpler objects. For example, integers are factored as products of primes and polynomials are factored as products of irreducible polynomials. We can say "the" factorization, because factorizations are unique in the integers and in the ring of polynomials over a field like the reals or the rational numbers. However, in many important contexts, factorization turns out not to be unique. Elements can have multiple, distinct factorizations, and even have factorizations involving different numbers of irreducibles. The contexts where one encounters nonunique factorization include algebraic number rings and Dedekind domains (a number theoretic context), subrings of polynomial rings and group rings (a commutative algebra context), and even submonoids of the integers (for example, the Money Changing Problem). Questions about nonunique factorization relate to additive number theory, additive combinatorics, and other areas of mathematics. This summer, we'll study properties of nonunique factorization in one of these contexts. The prerequisite for this project is a course in discrete mathematics or an introductory proofs course (familiarity with abelian groups or a course in abstract algebra or number theory is also recommended).

References:
[1] P. Baginski; S.T. Chapman, Factorizations of algebraic integers, block monoids, and additive number theory. Amer. Math. Monthly 118 (2011), no. 10, 901-920.
[2] L. Bryant; J. Hamblin; L.A. Jones, A variation on the money-changing problem. Amer. Math. Monthly 119 (2012), no. 5, 406-414.
[3] M. Jenssen; D. Montealegre; V. Ponomarenko, Irreducible factorization lengths and the elasticity problem within N. Amer. Math. Monthly 120 (2013), no. 4, 322-328.

Chaos and Integrability in Mathematical Billiards
Faculty Mentor: Mark Demers

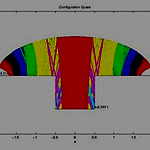
Mathematical billiards are systems of point particles colliding with fixed boundaries. Their importance to mathematical physics stems from the fact that they are the simplest mathematically solvable systems that model the transport of mass and energy from deterministic microscopic dynamics. The behavior of such systems is known to depend strongly on the geometric properties of the boundaries against which the particles collide: a range of dynamical behaviors from integrable to fully chaotic can be observed with relatively small changes to the boundary.

Students in this project will be introduced to the study of mathematical billiards in a variety of domains. We will approach these models both analytically and numerically. Specifically, we will focus on constructing domains in which integrable and chaotic components of the phase space coexist and study the boundary regions of these components. Important dynamical notions such as mixing, entropy and Lyapunov exponents will also be introduced and studied in this context.

A basic proof-writing course and a course in linear algebra are required. Experience with Matlab and courses in real analysis or probability theory are a plus.

References:
[1] N. Chernov and R. Markarian, Chaotic Billiards, Mathematical Surveys and Monographs, vol 127, American Mathematical Society, 2006, 316 pages.
[2] A. Katok and B. Hasselblatt, An Introduction to the Modern Theory of Dynamical Systems, Cambridge University Press, 1996, 824 pages.

Graph Theory and Commutative Algebra
Faculty Mentor: Janet Striuli

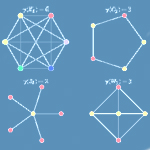
In this project, we will explore the connections between graph theory and commutative algebra. Graphs identify ideals in polynomial rings, and in particular so-called cover and edge ideals are the most studied. The study of the invariant associated to those ideals reveals properties of the original graph. For example, the coloring number is an invariant of the graph that has been detected (in many cases) by the stabilization number of the associated primes of powers of the cover ideal. My research group will study the relationship between cover ideals and graphs. A course in abstract algebra is the prerequisite for this project.

References:
[1] Chris A. Francisco, H.T. H`a and Adam Van Tuyl. Associated primes of monomial ideals and odd holes in graphs. J. Alg. Comb. 32 (2010), no. 2, 287-301.
[2] Chris A. Francisco, H.T. H`a and Adam Van Tuyl. A conjecture on critical graphs and connections to the persistence of associated primes. Discrete Math. 310 (2010), 2176-2182.
[3] Chris A. Francisco, H.T. H`a and Adam Van Tuyl. Coloring of hypergraphs, perfect graphs, and associated primes of powers of monomial ideals. J.Algebra 331 (2011), 224-244.
[4] H.T. H`a and S. Morey. Embedded associated primes of powers of square-free monomial ideals. J. Pure Appl. Algebra 214 (2010), no. 4, 301-308.
[5] J. Martinez-Bernal, S. Morey and R.H. Villarreal. Associated primes of powers of edge ideals. Collect. Math. 63 (2012), no. 3, 361-374.
[6] A beginner's Guide to Edge and Cover Ideals, Monomial Ideals, Computations and Applications, Lecture Notes in Mathematics Volume 2083, 2013, pp 63-94.